在大模型稀疏化架构的演进中,效率与性能的权衡始终是核心挑战。
MoE(Mixture of Experts)通过仅激活部分专家实现高效推理,但其频繁的跨专家参数访问带来了高昂的内存开销。为解决这一问题,早期提出的 Ultra sparse memory network(UltraMem) 采用类似机制,却以更低的内存访问成本实现了更快的推理速度。然而,它的性能仅相当于2专家MoE,难以满足高阶任务需求。
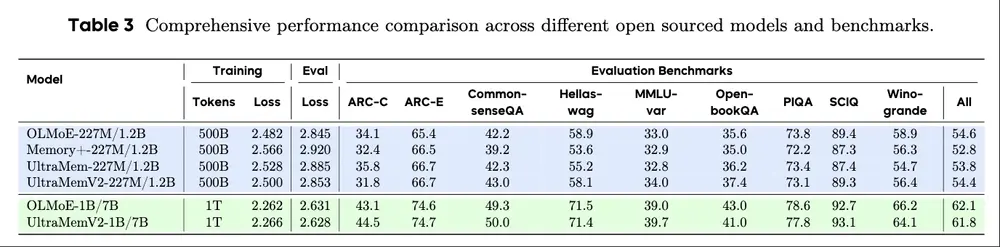
现在,字节跳动 Seed 项目组发布 UltraMemV2 —— 一种重新设计的内存网络架构,在保持极低内存访问的同时,性能已全面追平最先进的8专家MoE模型。

这不仅是一次架构迭代,更是对“稀疏即慢”这一固有认知的突破。
问题本质:稀疏 ≠ 高效
当前主流稀疏模型(如MoE)的核心思想是:
每个输入仅激活少量专家,从而减少计算量。
但现实是:
- 即使计算量下降,参数分布分散导致大量缓存未命中
- 频繁的内存读取成为瓶颈,尤其在长序列场景下
- 实际推理速度受限于内存带宽而非算力
UltraMem 的初衷正是应对这一瓶颈:它用一个集中式可寻址内存表替代分散专家,通过检索机制激活参数,大幅降低内存访问次数。
但初代 UltraMem 因表达能力不足,性能停滞在2专家MoE水平。
UltraMemV2 的目标很明确:
在不增加内存访问成本的前提下,提升表达能力,达到8专家MoE的性能上限。
架构创新:从“能用”到“好用”的五项关键改进
UltraMemV2 并非简单扩大内存表,而是在架构层面进行系统性重构。其核心改进包括:
1. 内存层深度集成
- 将内存层嵌入每一个 Transformer 块中
- 不再是外围增强模块,而是模型的基础记忆单元
- 每一层都能动态检索和更新长期语义信息
2. 简化隐式值扩展(IVE)
- 原始 IVE 使用复杂非线性映射扩展检索到的内存值
- UltraMemV2 改为单一线性投影,显著降低计算开销
- 实验表明,简单映射在多数任务中已足够有效
3. 基于 FFN 的值处理(借鉴 PEER)
- 引入轻量 FFN 结构处理检索后的内存值
- FFN 内部维度固定,参数效率高
- 在不增加稀疏激活参数的前提下提升非线性表达能力
4. 优化初始化策略
- 内存表与查询头的初始化经过精细调校
- 防止训练初期因检索偏差导致梯度爆炸或收敛困难
- 提升训练稳定性,支持更大规模部署
5. 计算比例再平衡
- 调整内存层与标准 FFN 的计算资源配比
- 避免内存层成为瓶颈或冗余组件
- 实现整体计算效率最优
这些改动共同构成了一个更紧凑、更稳定、更具表达力的稀疏记忆架构。
工作原理:如何实现“低访存、高性能”?
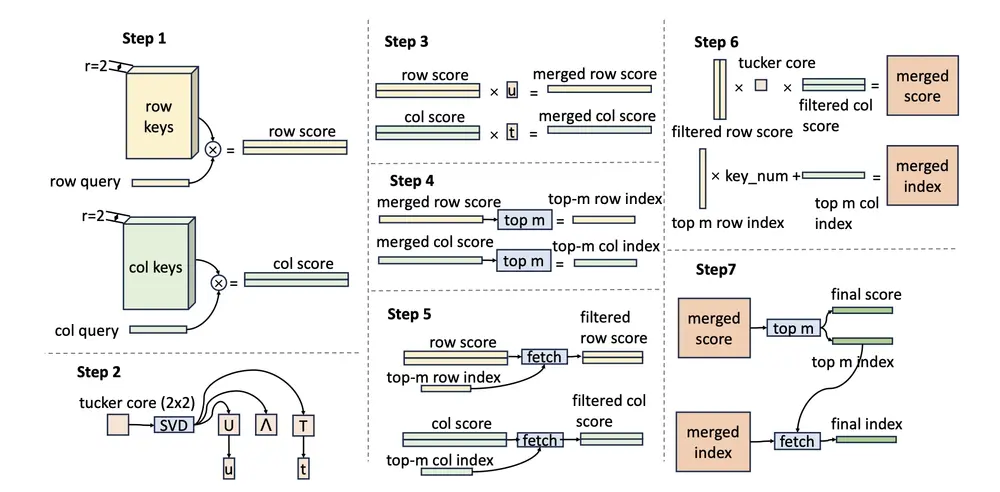
UltraMemV2 的工作流程如下:
- 查询生成
输入 token 经过查询头生成检索向量。 - Tucker 分解查询键检索(TDQKR)
使用 Tucker 分解压缩键空间,在降低存储成本的同时高效匹配最相关的内存条目。 - 值检索与扩展
检索出对应的内存值,通过线性投影 + 轻量 FFN 进行非线性变换。 - 融合输出
将处理后的值与主干网络输出融合,进入下一层。
整个过程仅需一次主内存访问,远少于 MoE 多专家并行读取的开销。
性能表现:追平MoE,超越在长序列
在相同计算预算和参数配置下,UltraMemV2 实现了与8专家MoE相当的整体性能,但在关键任务上显著领先:
| 任务 | 相比 MoE 提升 |
|---|---|
| 长文本记忆 | +1.6 个百分点 |
| 多轮对话记忆 | +6.2 个百分点 |
| 上下文学习(in-context learning) | +7.9 个百分点 |
这表明:UltraMemV2 不仅“跑得快”,而且“记得住”。
特别是在处理超过8K token 的长文档或多轮对话历史时,其内置记忆机制展现出更强的上下文保持能力。
可扩展性验证:支持超大规模模型
UltraMemV2 已在 1200亿参数 的大模型中完成验证:
- 每次推理仅激活 2.5B 参数
- 激活密度低至约 2%
- 训练稳定,性能随规模持续提升
更重要的是,实验发现:
激活参数的“质量”和“分布密度”对性能的影响,远大于总稀疏参数数量。
这意味着:通过更智能的检索机制和更高效的值处理,可以用更少的激活实现更好的效果。
应用场景
UltraMemV2 特别适用于以下场景:
✅ 长文本处理
- 法律合同、科研论文、小说章节等长文档理解与生成
- 支持跨段落语义关联,避免信息遗忘
✅ 多轮对话系统
- 在客服、虚拟助手等场景中,持续跟踪用户意图与历史上下文
- 减少重复提问,提升对话连贯性
✅ 资源受限部署
- 移动端、边缘设备等内存带宽受限环境
- 在低功耗下实现高质量推理
✅ 大规模预训练
- 作为 MoE 的替代架构,用于下一代百亿级以上语言模型
- 降低训练与推理的基础设施成本
相关文章