DeepSeek于4月30日发布了 DeepSeek-Prover-V2,这是一个专门用于 Lean 4 形式化定理证明的开源大语言模型。该模型的设计目标是将非形式化的数学推理与形式化的证明构建整合到一个统一的框架中,从而提高定理证明的效率和准确性。
1. 模型概述
通过递归证明搜索合成冷启动推理数据
为了构建冷启动数据集,DeepSeek 开发了一个递归定理证明流程,利用 DeepSeek-V3 作为子目标分解和形式化的统一工具。具体步骤如下:
- 子目标分解:DeepSeek-V3 被提示将复杂问题分解为高层次的证明草图,并在 Lean 4 中形式化这些证明步骤,生成一系列子目标。
- 证明搜索:使用一个较小的 7B 模型处理每个子目标的证明搜索,以降低计算负担。
- 合成冷启动数据:一旦复杂问题的分解步骤被解决,完整的逐步形式化证明与 DeepSeek-V3 的对应思维链配对,创建冷启动推理数据。
使用合成冷启动数据进行强化学习
- 筛选挑战性问题:从 7B 证明模型无法端到端解决但所有分解子目标均已成功解决的问题中筛选出一组挑战性问题。
- 构建完整证明:通过组合所有子目标的证明,构建原始问题的完整形式化证明,并将其添加到 DeepSeek-V3 的思维链中,生成非形式化推理与形式化的连贯合成。
- 强化学习阶段:在合成冷启动数据上微调证明模型后,进行强化学习阶段,进一步增强模型将非形式化推理与形式化证明构建连接的能力。主要奖励监督形式为二元正确或错误反馈。
2. 模型性能
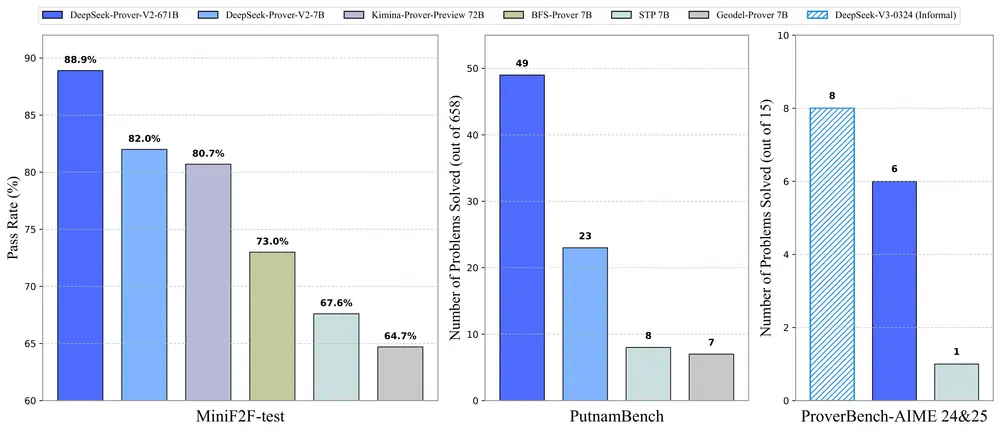
最终模型 DeepSeek-Prover-V2-671B 在神经定理证明中达到了最先进的性能:
- MiniF2F-test:实现 88.9% 的通过率。
- PutnamBench:在 658 个问题中解决了 49 个。
- 证明生成:为 miniF2F 数据集生成的证明可作为 ZIP 存档下载。
3. ProverBench:AIME 和教科书问题的形式化
DeepSeek 推出了 ProverBench,一个包含 325 个问题的基准数据集,旨在支持对高中竞赛问题和本科水平数学的更全面评估。其中:
- AIME 竞赛问题:15 个问题来自近期 AIME 竞赛(AIME 24 和 25)的数论和代数问题形式化,提供真实的高中竞赛级别挑战。
- 教科书问题:其余 310 个问题来自精选的教科书示例和教育教程,构成一个多样化且具有教学依据的形式化数学问题集合。
| Area | Count |
|---|---|
| AIME 24&25 | 15 |
| Number Theory | 40 |
| Elementary Algebra | 30 |
| Linear Algebra | 50 |
| Abstract Algebra | 40 |
| Calculus | 90 |
| Real Analysis | 30 |
| Complex Analysis | 10 |
| Functional Analysis | 10 |
| Probability | 10 |
| Total | 325 |
4. 模型与数据集下载
DeepSeek-Prover-V2 提供两种模型规模:
- DeepSeek-Prover-V2-671B:基于 DeepSeek-V3-Base 训练。
- DeepSeek-Prover-V2-7B:基于 DeepSeek-Prover-V1.5-Base 构建,支持高达 32K 令牌的扩展上下文长度。
| 模型 | 下载 |
|---|---|
| DeepSeek-Prover-V2-7B | HuggingFace |
| DeepSeek-Prover-V2-671B | HuggingFace |
| 数据 | 下载 |
|---|---|
| DeepSeek-ProverBench | HuggingFace |
5. 快速入门
DeepSeek-Prover-V2 可以直接使用 Hugging Face 的 Transformers 进行模型推理。DeepSeek-Prover-V2-671B 与 DeepSeek-V3 共享相同的架构。有关详细信息和支持功能,请参阅 Hugging Face 上的 DeepSeek-V3 文档。
总结
DeepSeek-Prover-V2 是一个创新的开源大语言模型,专为 Lean 4 形式化定理证明设计。通过递归证明搜索和强化学习,该模型能够将非形式化的数学推理与形式化的证明构建整合到一个统一的框架中。其在 MiniF2F-test 和 PutnamBench 上的卓越表现证明了其强大的定理证明能力。此外,ProverBench 的推出为高中竞赛问题和本科水平数学的评估提供了新的基准。DeepSeek-Prover-V2 的开源和易于使用的特性使其成为研究人员和开发者的理想选择。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
相关文章

暂无评论...