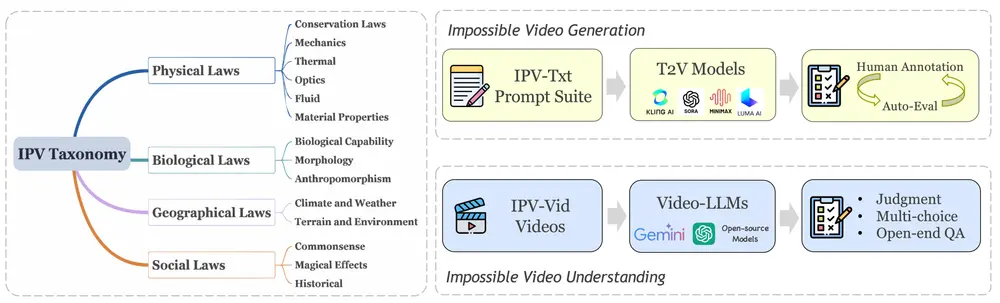
在大语言模型(LLM)的训练流程中,“后训练”(post-training)是连接预训练与实际应用的关键阶段。当前主流方法主要包括两类:监督微调(SFT)和强化学习(RL)。前者依赖高质量演示数据,强调“模仿”;后者通过环境反馈优化策略,注重“探索”。
然而,这两种方法常被视为对立路径——SFT稳定但缺乏创新,RL灵活但训练不稳定。如何融合二者优势,成为提升模型推理能力的重要课题。
近期,来自清华大学、上海AI实验室与微信AI的研究团队提出一个全新视角:SFT与RL并非割裂,而是同一优化过程的不同实现方式。基于这一洞察,他们构建了统一策略梯度估计器(Unified Policy Gradient Estimator, UPGE),并在此基础上推出了自适应训练算法——混合后训练(Hybrid Post-Training, HPT)。
该工作不仅提供了理论上的统一解释,也在多个数学推理任务中实现了性能突破。
问题本质:后训练的两大来源与两种路径
后训练的目标是让预训练模型更好地完成特定任务。其数据主要来自两个渠道:
- 离线数据:人类标注或强模型生成的高质量示范轨迹,常用于监督微调(SFT)。
- 在线数据:当前模型自行采样的输出轨迹,通常用于强化学习(如PPO、GRPO等)。
传统做法将两者分开处理:先SFT“打基础”,再RL“提能力”。但这种分阶段策略存在明显短板:
- SFT无法利用模型自身的探索结果;
- RL在早期阶段因采样质量差,容易引入噪声,导致训练不稳定;
- 二者之间缺乏动态协调机制,难以平衡“利用已有知识”与“探索新解法”。
研究团队认为,问题的关键不在于选择SFT还是RL,而在于能否从统一框架理解它们的本质联系。
理论突破:UPGE——一个可拆解的统一梯度形式
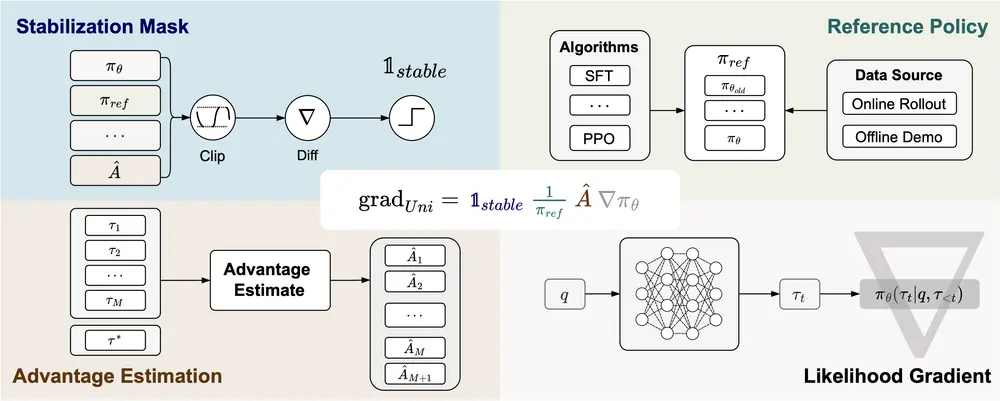
论文的核心贡献是提出了统一策略梯度估计器(UPGE),它将多种后训练方法的更新方向统一为如下形式:
∇J = E[ 掩码 × (优势估计) × (参考策略分母)⁻¹ × (似然梯度) ]
这个公式看似抽象,实则揭示了不同算法之间的内在一致性。UPGE由四个可替换模块构成:
| 模块 | 功能说明 | 不同方法的体现 |
|---|---|---|
| 稳定化掩码(Stabilization Mask) | 控制梯度更新范围,防止无效更新 | SFT中为全1;RL中可基于动作有效性设计 |
| 参考策略分母(Reference Policy Denominator) | 提供对比基准,控制方差 | SFT使用初始策略;RL使用上一轮策略 |
| 优势估计(Advantage Estimate) | 衡量动作优劣 | SFT中为常数;RL中为奖励减去基线 |
| 似然梯度(Likelihood Gradient) | 模型参数对输出概率的敏感度 | 所有方法共用 |
通过调整这四个组件的实现方式,SFT、PPO、DPO、GRPO等算法均可视为UPGE的特例。例如:
- 当优势估计设为常数、参考策略固定时,UPGE退化为SFT;
- 当优势来自蒙特卡洛回报、参考策略为上一轮模型时,即对应标准RL更新。
这一框架打破了SFT与RL的界限,也为设计更灵活的训练策略打开了空间。
算法创新:HPT——动态切换训练信号的混合策略
基于UPGE的理论洞察,团队提出了混合后训练(HPT)算法。其核心思想是:根据模型实时表现,动态决定使用SFT还是RL信号进行更新。
具体机制如下:
- 在训练过程中持续采样模型输出;
- 对每个问题,评估当前模型生成解法的质量(如是否通过验证);
- 若成功率低于阈值 → 增加SFT权重,借助高质量示范“纠偏”;
- 若表现良好 → 提高RL权重,鼓励探索更优路径。
这种自适应加权机制实现了两个关键目标:
- 保留已有能力:避免RL初期噪声破坏已掌握的推理模式;
- 促进有效探索:当模型具备一定基础后,允许其跳出示范数据限制,寻找新解法。
此外,HPT无需额外标注或复杂调度策略,可直接集成到现有训练流程中。
实验验证:在数学推理任务中全面领先
研究团队在六个数学推理基准和两个分布外(OOD)测试集上验证了HPT的有效性,涵盖Qwen和LLaMA系列多个模型规模。
1. 主流基准表现(以AIME 2024为例)
| 方法 | Qwen2.5-Math-7B (Pass@1) |
|---|---|
| SFT | 25.1 |
| GRPO | 19.4 |
| HPT | 33.0 |
HPT相较SFT提升近8个百分点,在其他数学任务(如MATH、AMC)中也保持一致领先。
2. 多模型泛化能力
| 模型 | HPT提升幅度(vs SFT) |
|---|---|
| Qwen2.5-Math-1.5B | +6.2 |
| Qwen2.5-Math-7B | +7.9 |
| LLaMA-3.1-8B | +5.3 |
表明HPT不仅适用于特定架构,且在小模型上收益更为显著。
3. 探索能力分析
在Pass@k指标(衡量多轮采样中最优解出现概率)上,HPT显著优于纯SFT和RL方法,说明其在解法多样性与最优性之间取得了更好平衡。
消融实验进一步证实:动态权重机制是性能提升的关键因素,固定权重组合无法达到同等效果。
意义与展望
HPT的价值不仅在于性能提升,更在于它体现了一种新的训练范式转变:
从“分阶段训练”走向“连续自适应学习”。
通过UPGE框架,SFT与RL不再是非此即彼的选择,而是可以根据数据质量和模型状态灵活调配的“训练资源”。这种统一视角有助于构建更高效、更鲁棒的后训练流程。
未来,这一思路可扩展至更多任务场景,如代码生成、对话系统、工具调用等,尤其适合那些需要兼顾稳定性与创新能力的应用。
相关文章