监督微调(SFT)正变得越来越重。
过去,SFT 只是大模型训练流程中的一个轻量级收尾步骤;如今,它已演变为一场计算密集型任务,其数据规模和训练成本常常逼近中期预训练阶段。在有限算力预算下,如何高效利用数据,成为对齐大型语言模型(LLM)的关键挑战。
而现有数据剪枝方法普遍存在一个问题:割裂操作。
它们要么只在样本层面做筛选(如丢弃“简单”或“难学”的样本),要么仅在令牌(token)级别进行压缩(如截断输入长度)。这种分离式设计导致两个维度无法协同优化——高价值样本可能仍包含大量冗余 token,而精细的 token 剪枝又可能误删关键指令信号。
为打破这一瓶颈,来自上海交通大学 EPIC 实验室、阿里巴巴集团、南京大学、北京交通大学与香港科技大学的研究团队提出了一种全新视角:
将样本与令牌剪枝统一建模为一个联合优化问题。
他们推出了名为 Q-Tuning(Quadrant-based Tuning) 的新方法,并引入 错误-不确定性(Error-Uncertainty, EU)平面 作为诊断工具,系统化指导剪枝决策。
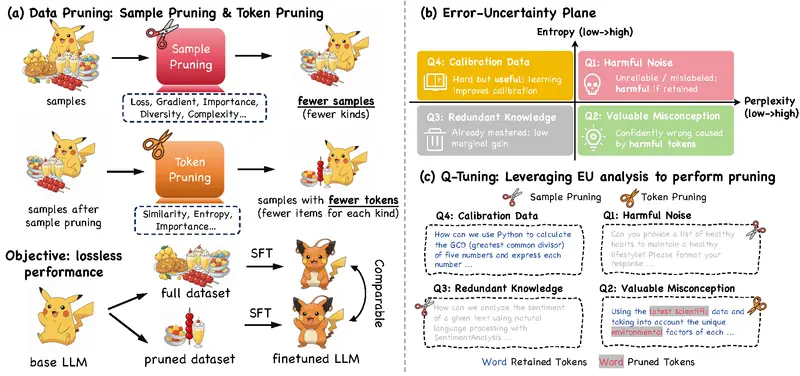
实验表明,Q-Tuning 不仅显著降低数据用量,还能反超全量训练的表现。
核心思想:从“怎么剪”到“为什么剪”
传统剪枝策略多依赖启发式规则,例如:
- 按困惑度(PPL)高低判断样本难度
- 按注意力权重或梯度大小决定保留哪些 token
但这些方法缺乏统一解释框架,难以回答:什么样的数据才是真正有价值的?
为此,Q-Tuning 提出使用两个正交指标构建二维分析空间——EU 平面:
| 维度 | 衡量内容 | 指标 |
|---|---|---|
| 错误轴(Error) | 模型是否预测错误 | 困惑度(Perplexity, PPL) |
| 不确定性轴(Uncertainty) | 模型是否犹豫不决 | 预测熵(Entropy, Ent) |
每个训练样本都可以被映射到该平面上的一个点,进而划分为四个象限:
| 象限 | 特征 | 是否保留 |
|---|---|---|
| Q1:高错误 + 高不确定性 | 混乱噪声,模型既错又不确定 | ❌ 删除 |
| Q2:高错误 + 低不确定性 | “自信地犯错” —— 存在校准偏差,但蕴含学习信号 | ✅ 保留 |
| Q3:低错误 + 高不确定性 | 正确但犹豫,可能是冗余知识 | ❌ 删除 |
| Q4:低错误 + 低不确定性 | 已掌握的知识,稳定且准确 | ✅ 保留 |
这个划分揭示了一个重要洞察:
最有价值的数据不是最难的,也不是最简单的,而是那些模型“自信地错了”的样本(Q2)——它们暴露了系统性的偏差,正是需要纠正的地方。
Q-Tuning:两阶段协调剪枝策略
基于 EU 平面的分析,Q-Tuning 设计了两个阶段的剪枝流程,实现样本与 token 的动态协同优化。
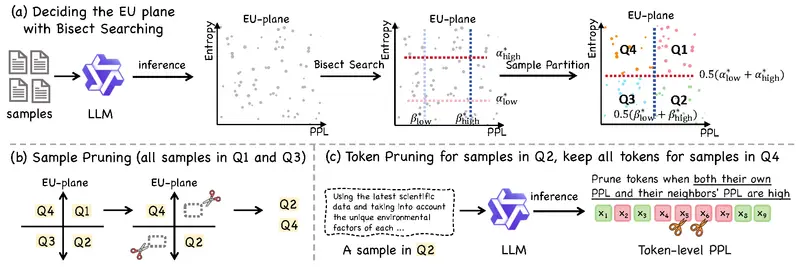
第一阶段:样本筛选(Sample Pruning)
根据 EU 象限分类,仅保留 Q2 和 Q4 中的样本:
- Q2:包含可纠正的误解,是模型改进的核心驱动力
- Q4:代表已掌握的知识,有助于保持输出稳定性
剔除 Q1(噪声)和 Q3(冗余),大幅减少无效计算。
第二阶段:非对称令牌剪枝(Asymmetric Token Pruning)
这是 Q-Tuning 的关键创新:不同类型的样本采用不同的 token 剪枝策略。
- 对于 Q2 样本(有价值误解):
使用上下文感知评分机制,识别并移除其中不重要的中间 token(如填充词、重复描述),保留开头指令和结尾正确响应等关键部分。 - 对于 Q4 样本(校准数据):
完整保留所有 token,确保模型不会因过度剪枝而遗忘已有能力。
这种“区别对待”的方式,在提升效率的同时,避免了传统剪枝中常见的性能退化问题。
实测表现:少用数据,反而更强
研究人员在多个主流模型和基准上验证了 Q-Tuning 的有效性,结果令人印象深刻:
| 模型 | 数据用量 | 性能表现 | 相比全数据基线 |
|---|---|---|---|
| SmolLM2-1.7B | 12.5% | 平均 +38% | ✅ 显著超越 |
| LLaMA2-7B | 25% 样本 + 70% token | 36.9(AlpacaEval) | ≈ 全量效果 |
| Mistral-7B | 同上 | 46.2 | ✅ 略优于全量 |
| LLaMA3-8B (GSM8K) | 35% 数据 | 48.07 | ✅ 超过全量训练 |
📌 在 SmolLM2 上,仅用八分之一的数据,平均性能提升近四成——这不仅是效率胜利,更是质量突破。
此外,在相同预算下,Q-Tuning 始终优于 InfoBatch、PPL-based Pruning、SparseVLM 等现有方法,证明其联合优化策略的有效性。
消融实验:为何必须“联合剪枝”?
研究者通过对比实验进一步验证了核心假设:
- 仅做样本剪枝(保留所有 token):Q-Tuning 优于所有基线 → 说明样本选择有效
- 仅做 token 剪枝(保留所有样本):Q-Tuning 依然领先 → 表明 token 评分机制精准
- 两者结合时性能最大 → 验证了“协调决策”带来的增益
这也解释了为什么孤立剪枝难以突破瓶颈:样本和 token 层面的信息互补,必须统一考虑。
主要贡献总结
- 提出 EU 平面:首个用于诊断 SFT 数据效用的二维分析框架,揭示了传统剪枝失败的原因。
- 形式化联合剪枝问题:将样本与 token 剪枝建模为双层优化任务,奠定理论基础。
- 推出 Q-Tuning 算法:首个基于诊断驱动的动态剪枝方法,实现样本与 token 协同优化。
- 开源实践价值:适用于各类 LLM 架构,在低预算场景下提供高性能微调路径。
相关文章