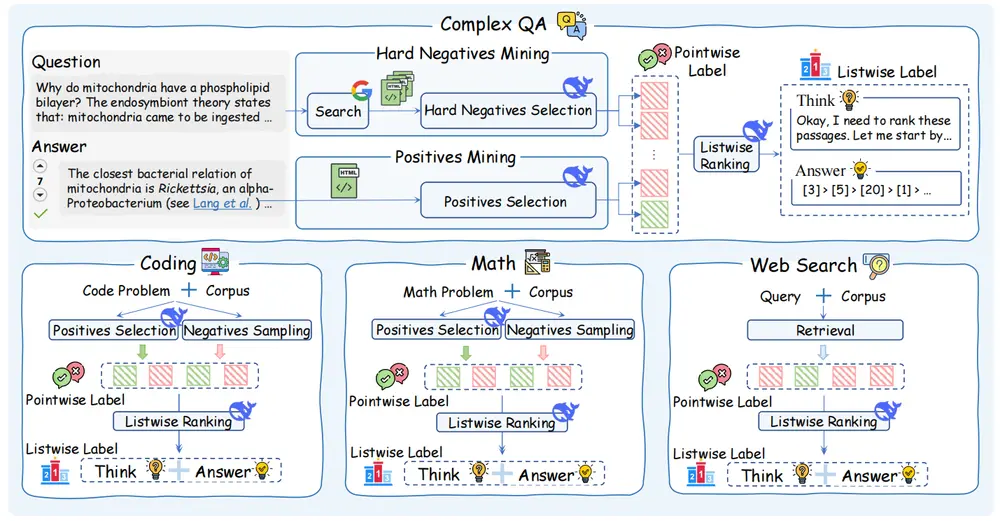
近日,由普林斯顿大学语言与智能实验室、清华大学、英伟达、斯坦福大学、Meta FAIR、亚马逊、上海交通大学和北京大学联合研发的 Goedel-Prover-V2 正式发布。这是一系列开源语言模型,在自动形式化数学证明生成领域树立了新的技术标杆。
- 项目主页:https://blog.goedel-prover.com
- Goedel-Prover-V2-32B:https://huggingface.co/Goedel-LM/Goedel-Prover-V2-32B
- Goedel-Prover-V2-8B:https://huggingface.co/Goedel-LM/Goedel-Prover-V2-8B
Goedel-Prover-V2 采用专家迭代 + 强化学习的训练流水线,引入三项关键创新:
- 分层数据合成:生成难度递增的训练任务,逐步提升模型能力
- 验证器引导的自我纠正:通过 Lean 编译器反馈,模拟人类“试错-修正”的证明优化过程
- 模型平均技术:融合多个训练检查点,提升鲁棒性与最终性能
这一成果不仅在多个权威基准测试中超越了当前最先进的模型,更在模型规模远小于竞品的情况下实现了相当甚至更优的性能表现。
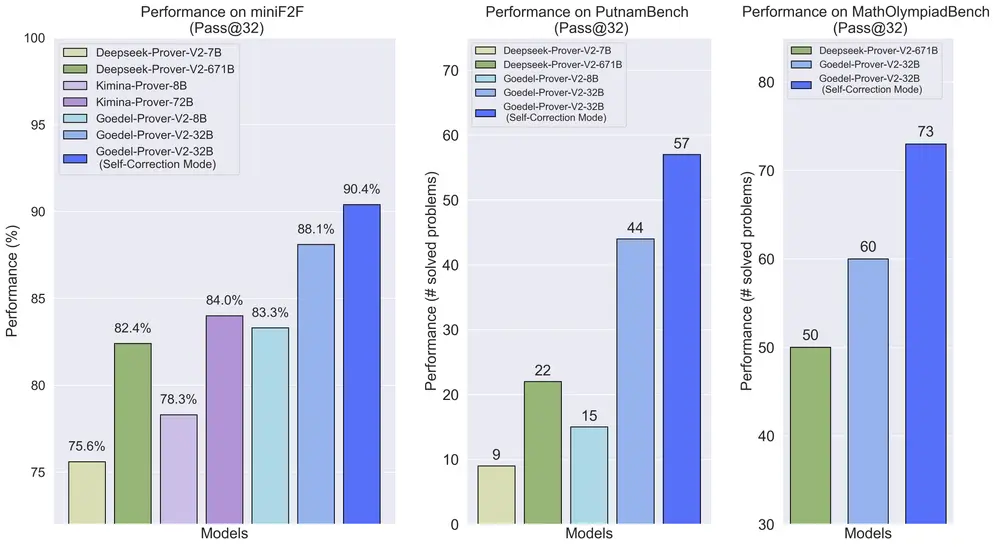
性能突破:小型模型匹敌超大模型,旗舰模型登顶榜单
Goedel-Prover-V2 系列包括两个主要版本:
- Goedel-Prover-V2-8B(80亿参数)
- Goedel-Prover-V2-32B(320亿参数)
在MiniF2F测试集上的表现如下:
| 模型 | 模式 | Pass@32 成功率 |
|---|---|---|
| DeepSeek-Prover-V2-671B | 标准 | 83.3% |
| Goedel-Prover-V2-8B | 标准 | 83.3% |
| Goedel-Prover-V2-32B | 标准 | 88.1% |
| Goedel-Prover-V2-32B | 自我纠正 | 90.4% |
值得注意的是,Goedel-Prover-V2-8B 虽然参数规模仅为 DeepSeek-Prover 的 1/100,却在性能上完全匹敌,展现了其极高的训练效率和模型压缩潜力。
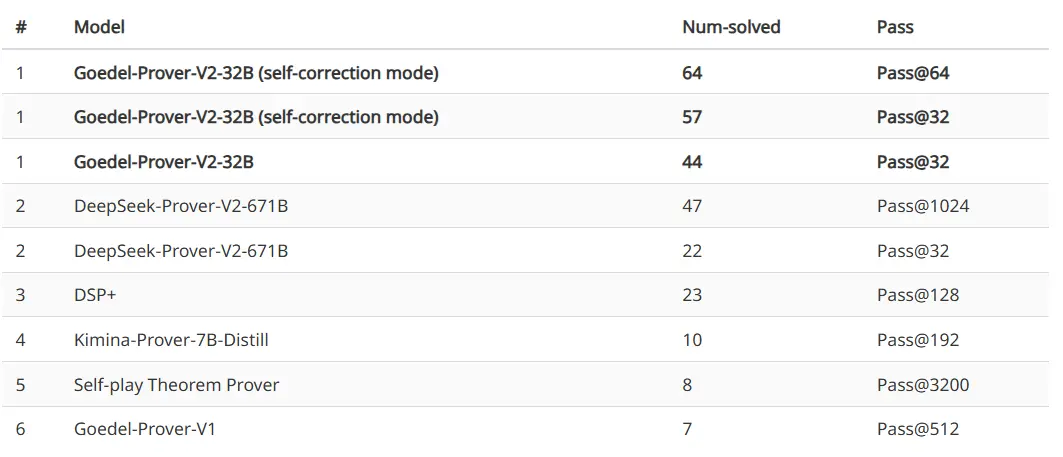
在更具挑战的 PutnamBench 数据集上,Goedel-Prover-V2-32B 在自我纠正模式下以 Pass@64 解决了 64 个问题,位居排行榜首位,远超 DeepSeek-Prover-V2-671B 在 Pass@1024 下解决 47 个问题的记录。
自我纠正机制:模拟人类“试错”思维,显著提升证明质量
Goedel-Prover-V2 引入了一种验证器引导的自我纠正机制。其核心流程如下:
- 模型生成初始证明
- 利用 Lean 编译器进行验证
- 根据反馈进行迭代修正(最多两轮)
- 最终输出更高质量的证明
尽管引入了两轮修正,整体输出长度仅从标准的 32K token 增加到 40K token,计算效率依然保持高效。
这种机制模拟了人类在数学证明中不断试错、改进的思维过程,为自动证明生成系统提供了更接近人类推理的能力。
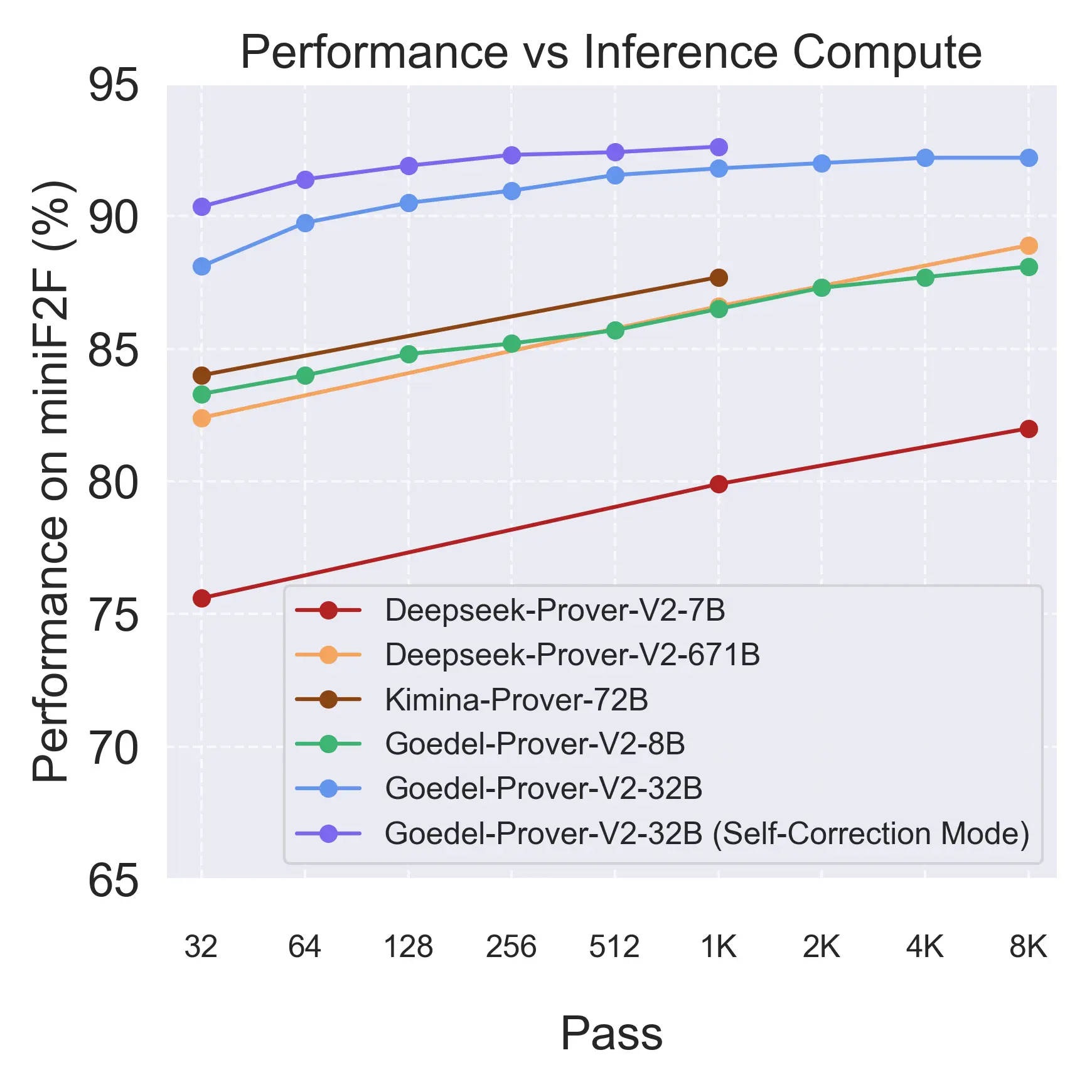
推理时间扩展:持续领先,越算越强
Goedel-Prover-V2-32B 在不同推理时间预算下的表现始终优于此前的技术标杆模型,展现了其在长时间、多步推理任务中的稳定性与扩展性。
技术方法详解
Goedel-Prover-V2 基于 Qwen3-8B 和 Qwen3-32B 模型构建,采用标准的专家迭代与强化学习流程:
- 形式化问题输入
- 生成候选证明
- 使用 Lean 编译器验证
- 将新发现的正确证明加入训练集
- 通过强化学习进一步优化模型
在此基础上,团队引入三项关键创新:
1. 分层数据合成(Hierarchical Data Synthesis)
自动生成介于简单与复杂之间的中级问题,构建更平滑的难度梯度,提供更密集、信息更丰富的训练信号,帮助模型逐步掌握复杂定理的证明能力。
2. 验证器引导的自我纠正(Validator-Guided Self-Correction)
训练模型有效利用 Lean 编译器反馈,对初始证明进行迭代修正。该机制不仅提升了证明质量,还被整合到监督微调与强化学习阶段,形成闭环优化。
3. 模型平均(Model Averaging)
为防止后期训练中模型多样性下降,团队采用模型检查点与基模型的平均策略。这一简单但有效的方法显著提升了在高 K 值下的 Pass@K 性能。
开源发布:推动形式化验证与自动证明研究
Goedel-Prover-V2 团队已开源其模型,并发布了一个全新的基准数据集:
🔢 MathOlympiadBench
这是一个由人工验证的数学奥林匹克竞赛问题构成的形式化数据集,包含:
- ✅ 1959–2024 年 158 个 IMO 问题
- ✅ 2006–2023 年 131 个 IMO 短名单问题
- ✅ 68 个区域数学奥林匹克问题
- ✅ 3 个额外数学谜题
总计 360 个问题,全部以 Lean4 格式呈现,来源于 Compfiles 和 IMOSLLean4 仓库。
该数据集的发布旨在推动更多开源项目,特别是在IMO 竞赛自动求解系统方向的发展。
相关文章